Derivatives. Part 4. Instantaneous Velocity and Acceleration YouTube

In one dimension, one can say "velocity is the derivative of distance" because the directions are unambiguous. In higher dimensions it is more correct to say it is the derivative of position. One can also say that it is the derivative of displacement because those two derivatives are identical.
PPT 3.1 Derivative of a Function PowerPoint Presentation, free download ID1714674

And acceleration you can view as the rate of change of velocity with respect to time. So acceleration as a function of time is just going to be the first derivative of velocity with respect to time which is equal to the second derivative of position with respect to time. It's just going to be the derivative of this expression.
How To Calculate Average Velocity Calculus Haiper

Another use for the derivative is to analyze motion along a line. We have described velocity as the rate of change of position. If we take the derivative of the velocity, we can find the acceleration, or the rate of change of velocity. It is also important to introduce the idea of speed, which is the magnitude of velocity. Thus, we can state.
Velocity time graph, Displacement time graph & Equations Physics Aakash Byjus AESL
We observe that this velocity is negative, indicating (as expected) that the object is falling down. Figure \(4.1\) illustrates the relationship between the displacement, velocity and acceleration as functions of time. Figure 4.1: The position, velocity, and acceleration of an object that is thrown upwards and falls under the force of gravity.
What is Velocity? Definition, SI Unit, Examples & Applications The Engineering Projects

Velocity is the rate of change of a function. And rate of change is code for take a derivative. The velocity of an object is the derivative of the position function. You should have been given some function that models the position of the object. Take the derivative of this function.
Please explain 2nd step of equation dx instantaneous velocity, v = v = 12t+3 at t = 5 s, v

It's not division, it's the chain rule. Both the position and the velocity are differentiable because we know that dx dt = v d x d t = v and dv dt = a d v d t = a. That's what justifies the step. @JohnDouma Written as the chain rule, it would be d dtv(x) = dv dx dx dt d d t v ( x) = d v d x d x d t.
Velocity by Integration, II

Derivatives with respect to time. In physics, we are often looking at how things change over time: Velocity is the derivative of position with respect to time: v(t) = d dt(x(t)) v ( t) = d d t ( x ( t)) . Acceleration is the derivative of velocity with respect to time: a(t) = d dt(v(t)) = d2 dt2 (x(t)) a ( t) = d d t ( v ( t)) = d 2 d t 2 ( x.
Position Velocity Acceleration Derivative Form Stock Vector (Royalty Free) 1974352121 Shutterstock

As previously mentioned, the derivative of a function representing the position of a particle along a line at time t is the instantaneous velocity at that time. The derivative of the velocity, which is the second derivative of the position function, represents the instantaneous acceleration of the particle at time t.. If y = s(t) represents the position function, then v = s′(t) represents.
PPT Higher order derivatives PowerPoint Presentation, free download ID6250616

Explain the difference between average velocity and instantaneous velocity. Estimate the derivative from a table of values. Tangent Lines. We define the tangent line to the graph of a function as follows.. Velocity is the rate of change of position. As such, the velocity \(v(t)\) at time \(t\) is the derivative of the position \(s(t)\) at.
Derivatives of position, velocity, and acceleration in physics. YouTube

So, you differentiate position to get velocity, and you differentiate velocity to get acceleration. Here's an example. A yo-yo moves straight up and down. Its height above the ground, as a function of time, is given by the function, where t is in seconds and H ( t) is in inches. At t = 0, it's 30 inches above the ground, and after 4 seconds.
Derivation of Position Velocity Relation by Graphical Method YouTube

To find velocity, take the derivative of your original position equation. Speed is the absolute value of velocity.. To find acceleration, take the derivative of velocity. Using the position function to find velocity and acceleration . Take the course Want to learn more about Calculus 1? I have a step-by-step course for that. :)
Derivative of the Position Vector. Motion Along a Straight Line YouTube
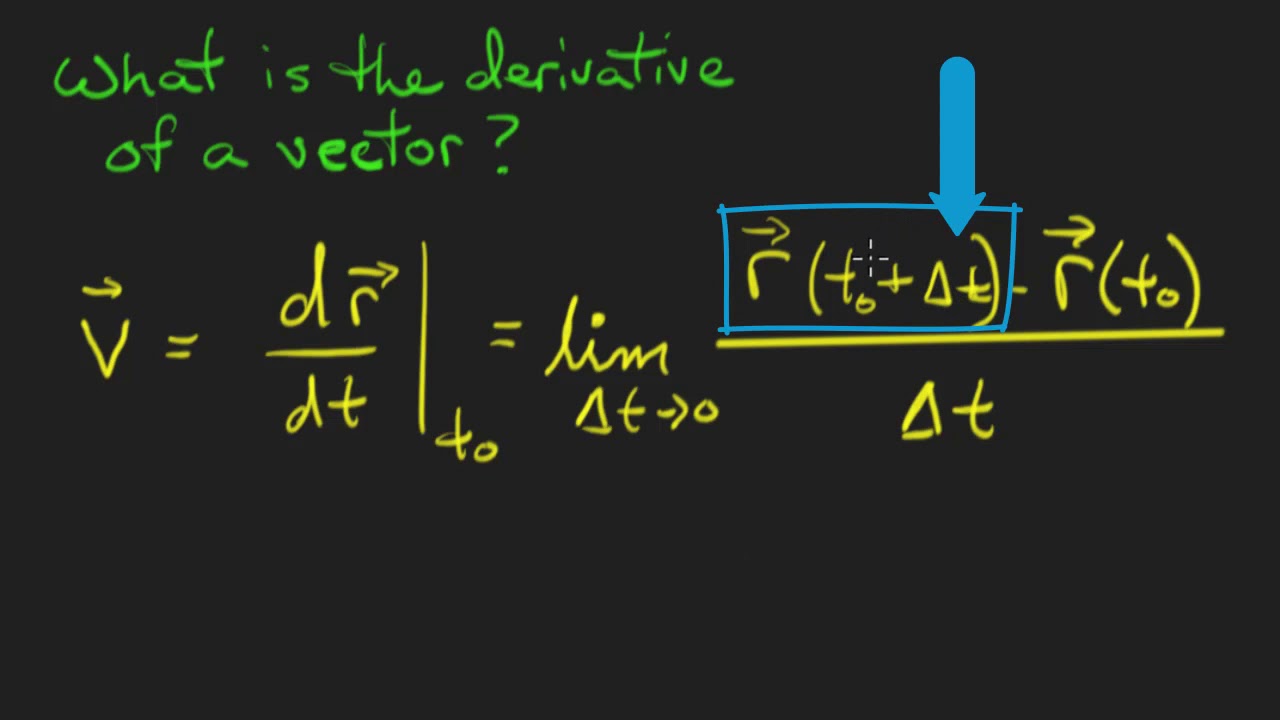
It's just the derivative of velocity, which is the second derivative of our position, which is just going to be equal to the derivative of this right over here. And so I'm just going to get derivative of three t squared with respect to t is six t. Derivative of negative eight t with respect to t is minus eight. And derivative of a constant is zero.
Displacement, velocity and acceleration using derivatives YouTube

Fourth derivative (snap/jounce). Snap, or jounce, is the fourth derivative of the position vector with respect to time, or the rate of change of the jerk with respect to time. Equivalently, it is the second derivative of acceleration or the third derivative of velocity, and is defined by any of the following equivalent expressions:
Find the velocity function by limit definition and use to evaluate the derivative at given

Motion graphs and derivatives. The green line shows the slope of the velocity-time graph at the particular point where the two lines touch. Its slope is the acceleration at that point. In mechanics, the derivative of the position vs. time graph of an object is equal to the velocity of the object. In the International System of Units, the.
classical mechanics What is the derivative of velocity with respect to position? Physics

The velocity tells us: how fast an object is moving. in which direction is the object moving. The fact that velocity is a vector is pretty important: traveling at 60 mph due East is not at all the same thing as traveling 60 mph due North! For this reason, in physics we make a distinction between the words velocity and speed.
Position and Displacement Equation (for Constant Velocity Motion) explanation & solving a

Well, you know that velocity is the derivative of position/distance, since it defines a rate (think meters travelled, distance, changing to m/s, a rate at which an object travels). Velocity also gives the slope of a distance vs. time graph, since you take how many units are travelled over a specific time parameter. Since an integral is the.